Weyl semimetals from spontaneous inversion symmetry breaking in pyrochlore oxides
Abstract
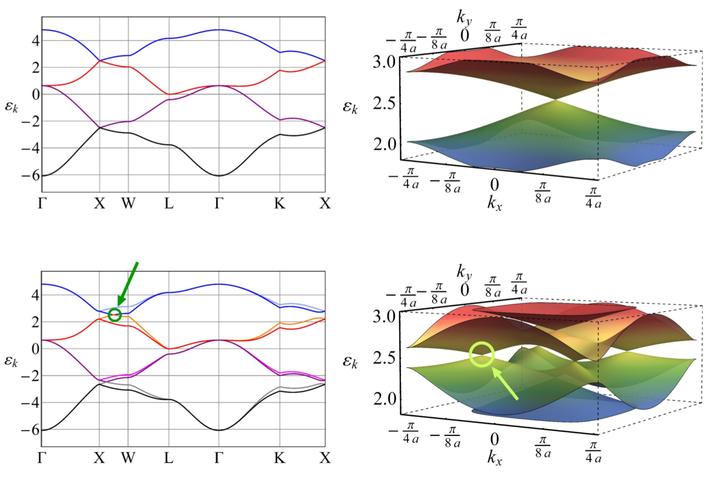
We study the electronic properties of strongly spin-orbit coupled electrons on the elastic pyrochlore lattice. Akin to the Peierls transition in one-dimensional systems, the coupling of the lattice to the electronic degrees of freedom can stabilize a spontaneous deformation of the crystal. This deformation corresponds to a breathing mode, which breaks the inversion symmetry. We find that for intermediate values of the staggered strain, the inversion-symmetry broken phase realizes a topological Weyl semimetal. In the temperature-elasticity phase diagram, the Weyl semimetal shows a reentrant phase behavior: it can be reached from a symmetric phase realized both at higher and at lower temperatures. The symmetric phase is a Dirac semimetal, which is protected by the nonsymmorphic space group of the pyrochlore lattice. Beyond a critical value of the staggered strain, the symmetry-broken phase is a fully gapped trivial insulator. The surface states of the Weyl semimetal form open Fermi arcs and we observe that their connectivity depends on the termination of the crystal. In particular, for the {111} films, the semiclassical closed electronic orbits of the surface states in a magnetic field cross the bulk either twice, four, six, or twelve times. We demonstrate how one can tune the number of bulk crossings through a Lifshitz-like transition of the Fermi arcs, which we call Weyl-Lifshitz transition, by applying a surface potential. Our results offer a route to a topological Weyl semimetal in nonmagnetic materials and might be relevant for pyrochlore oxides with heavy transition-metal ions such as alloys of iridates.