Abstract
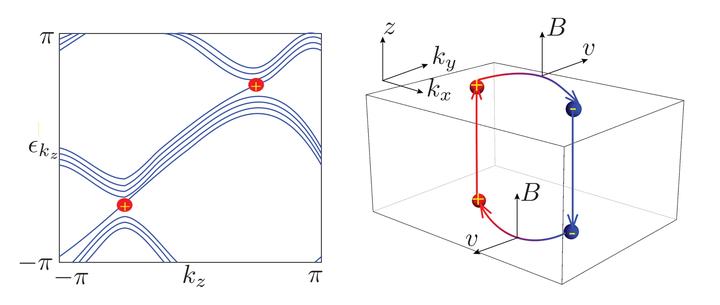
We show that the Nielsen-Ninomiya no-go theorem still holds on a Floquet lattice: there is an equal number of right-handed and left-handed Weyl points in a three-dimensional Floquet lattice. However, in the adiabatic limit, where the time evolution of the low-energy subspace is decoupled from the high-energy subspace, we show that the bulk dynamics in the low-energy subspace can be described by Floquet bands with extra left- or right-handed Weyl points, despite the no-go theorem. Assuming adiabatic evolution of two bands, we show that the difference of the number of right-handed and left-handed Weyl points equals twice the winding number of the adiabatic Floquet operator over the Brillouin zone. Based on these findings, we propose a realization of purely left- or right-handed Weyl particles on a 3D lattice using a Hamiltonian obtained through dimensional reduction of a four-dimensional quantum Hall system. We argue that the breakdown of the adiabatic approximation on the surface facilitates unusual closed orbits of wave packets in an applied magnetic field, which traverse alternatively through the low-energy and high-energy sector of the spectrum.