Abstract
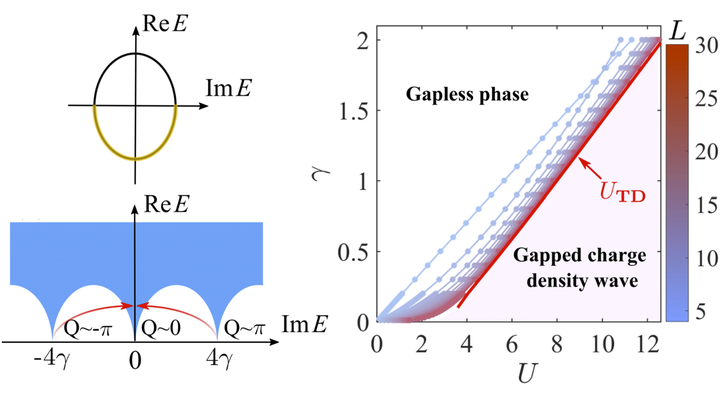
We study the Hatano-Nelson model, i.e., a one-dimensional non-Hermitian chain of spinless fermions with nearest-neighbor nonreciprocal hopping, in the presence of repulsive nearest-neighbor interactions. At half filling, we find two $\mathcal{PT}$ transitions, as the interaction strength increases. The first transition is marked by an exceptional point between the first and the second excited state in a finite-size system and is a first-order symmetry-breaking transition into a charge-density wave regime. Persistent currents characteristic of the Hatano-Nelson model abruptly vanish at the transition. The second transition happens at a critical interaction strength that scales with the system size and can thus only be observed in finite-size systems. It is characterized by a collapse of all energy eigenvalues onto the real axis. We further show that in a strong interaction regime, but away from half filling, the many-body spectrum shows point gaps with nontrivial winding numbers, akin to the topological properties of the single-particle spectrum of the Hatano-Nelson chain, which indicates the skin effect of extensive many-body eigenstates under open boundary conditions. Our results can be applied to other models such as the non-Hermitian Su-Schrieffer-Heeger-type model and contribute to an understanding of fermionic many-body systems with non-Hermitian Hamiltonians.