Superconductivity in hyperbolic spaces: Regular hyperbolic lattices and Ginzburg-Landau theory
Abstract
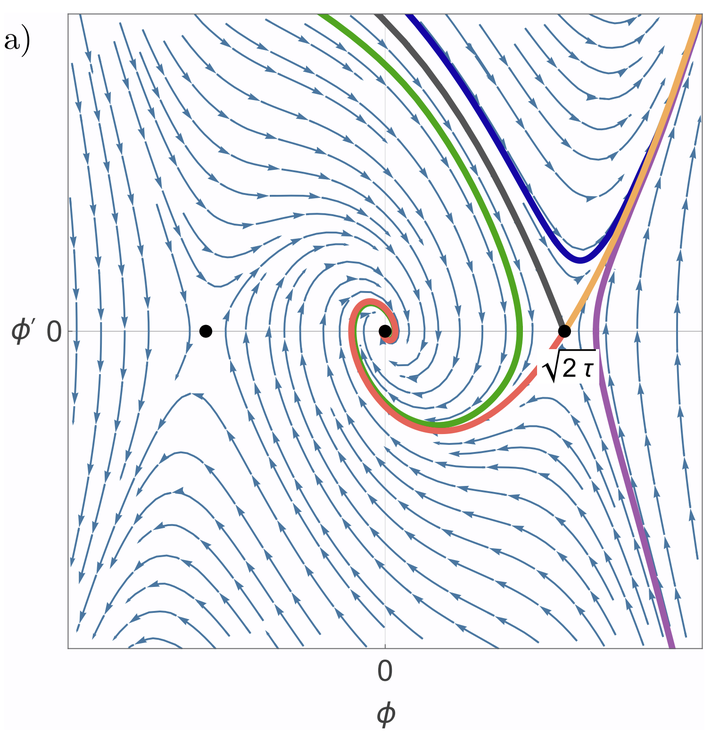
We study $s$-wave superconductivity in hyperbolic spaces using the Bogoliubov-de Gennes theory for discrete hyperbolic lattices and the Ginzburg-Landau theory for the continuous hyperbolic plane. Hyperbolic lattices maintain a finite fraction of boundary sites regardless of system size, thus fundamentally altering superconductivity through enhanced boundary effects absent in flat space. Within the BCS framework for hyperbolic lattices, uniform systems reproduce standard bulk behavior, whereas finite systems with open boundaries, studied through exact diagonalization and Cayley-tree approximations, exhibit boundary-enhanced superconductivity and boundary-only superconducting states that persist above the bulk critical temperature. Numerical studies further reveal that boundary termination critically determines superconducting properties; in particular, rough boundaries with dangling bonds generate zero-energy modes that raise critical temperatures by several times relative to smooth boundaries. Turning to the complementary Ginzburg-Landau analysis of the hyperbolic plane, we find that finite geometries permit radial variations of the condensate absent in infinite space. Owing to the interplay between coherence length and curvature radius, the theory exhibits two types of superconductivity even without magnetic fields, with vortices replaced by lines of vanishing order parameter in the nontrivial type. Our findings establish hyperbolic geometry as a platform for engineering boundary-controlled superconductivity, opening new directions for physics in curved spaces in condensed matter and holography.