Abstract
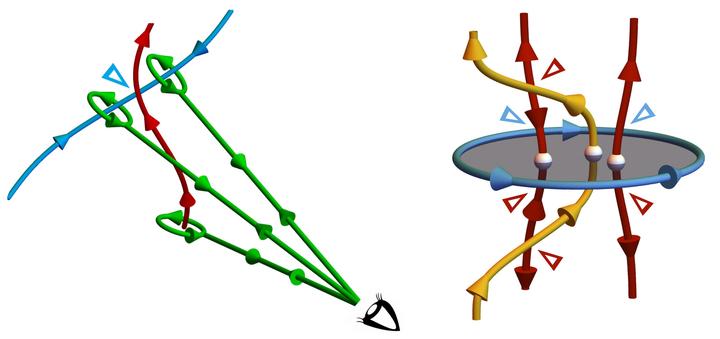
Nodal lines inside the momentum space of three-dimensional crystalline solids are topologically stabilized by a $\pi$-flux of Berry phase. Nodal-line rings in $\mathcal{PT}$-symmetric systems with negligible spin-orbit coupling (here described as “nodal class AI”) can carry an additional “monopole charge,” which further enhances their stability. Here, we relate two recent theoretical advancements in the study of band topology in nodal class AI. On the one hand, cohomology classes of real vector bundles were used to relate the monopole charge of nodal-line rings to their linking with nodal lines formed among the occupied and among the unoccupied bands. On the other hand, homotopy studies revealed that the generalization of the Berry-phase quantization to the case of multiple band gaps defines a non-Abelian topological charge, which governs the possible deformations of the nodal lines. The present work has three aims. First, we present how to efficiently wield the recently discovered non-Abelian topological charge. Second, we apply these methods to present an independent proof of the relation between the monopole charge and the linking structure, including all the fragile-topology exceptions. Finally, we show that the monopole charge flips sign when braided along a path with a nontrivial Berry phase. This facilitates a new type non-Abelian “braiding” of nodal-line rings inside the momentum space, that has not been previously reported. The work begins with a brief review of $\mathcal{PT}$-symmetric band topology, and the geometric arguments employed in our theoretical analysis are supplemented in the appendices with formal mathematical derivations.