Non-Abelian reciprocal braiding of Weyl nodes and its manifestations in ZrTe
Abstract
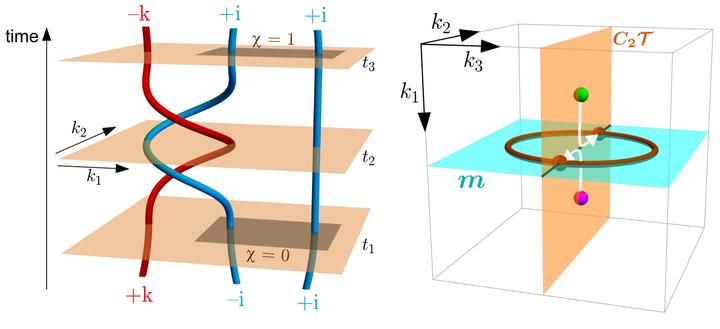
Weyl semimetals in three-dimensional crystals provide the paradigm example of topologically protected band nodes. It is usually taken for granted that a pair of colliding Weyl points annihilate whenever they carry opposite chiral charge. In stark contrast, here we report that Weyl points in systems that are symmetric under the composition of time reversal with a π rotation are characterized by a non-Abelian topological invariant. The topological charges of the Weyl points are transformed via braid phase factors, which arise upon exchange inside symmetric planes of the reciprocal momentum space. We elucidate this process with an elementary two-dimensional tight-binding model that is implementable in cold-atom set-ups and in photonic systems. In three dimensions, interplay of the non-Abelian topology with point-group symmetry is shown to enable topological phase transitions in which pairs of Weyl points may scatter or convert into nodal-line rings. By combining our theoretical arguments with first-principles calculations, we predict that Weyl points occurring near the Fermi level of zirconium telluride carry non-trivial values of the non-Abelian charge, and that uniaxial compression strain drives a non-trivial conversion of the Weyl points into nodal lines.