Abstract
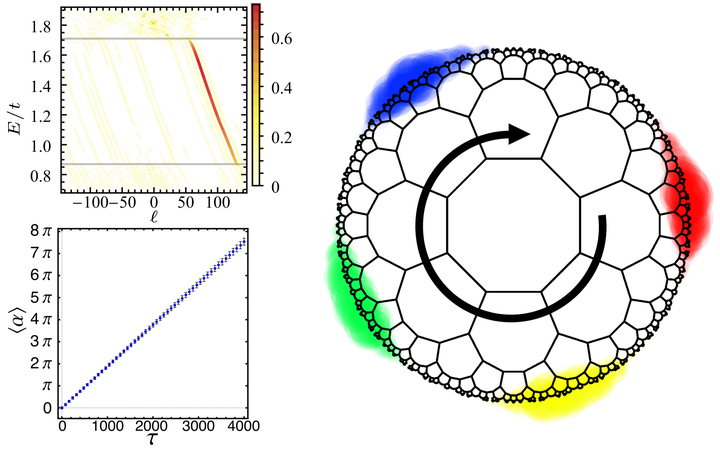
Recently, hyperbolic lattices that tile the negatively curved hyperbolic plane emerged as a new paradigm of synthetic matter, and their energy levels were characterized by a band structure in a four- (or higher-) dimensional momentum space. To explore the uncharted topological aspects arising in hyperbolic band theory, we here introduce elementary models of hyperbolic topological band insulators: the hyperbolic Haldane model and the hyperbolic Kane-Mele model; both obtained by replacing the hexagonal cells of their Euclidean counterparts by octagons. Their nontrivial topology is revealed by computing topological invariants in both position and momentum space. The bulk-boundary correspondence is evidenced by comparing bulk and boundary density of states, by modeling propagation of edge excitations, and by their robustness against disorder.