Abstract
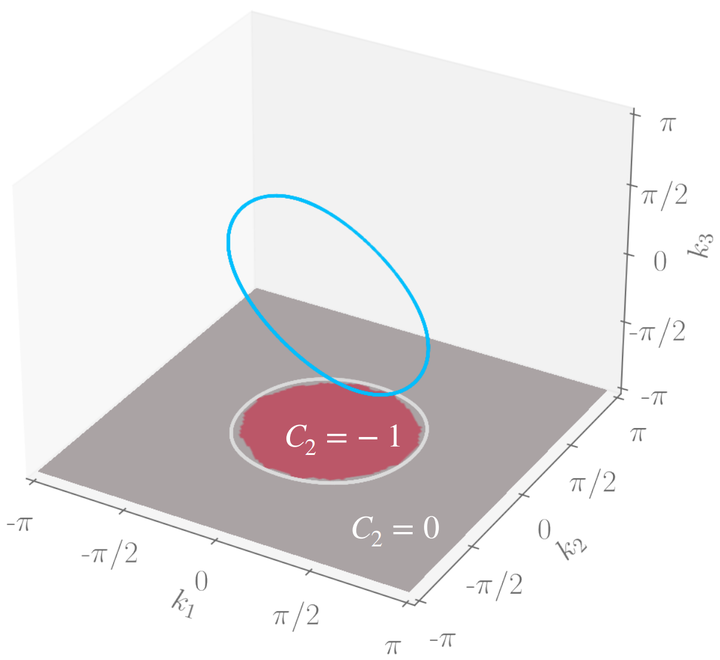
We extend the notion of topologically protected semi-metallic band crossings to hyperbolic lattices in negatively curved space. Due to their distinct translation group structure, such lattices support non-Abelian Bloch states which, unlike conventional Bloch states, acquire a matrix-valued Bloch factor under lattice translations. Combining diverse numerical and analytical approaches, we uncover a quartic scaling in the density of states at low energies, and illuminate a nodal manifold of codimension five in the reciprocal space. The nodal manifold is topologically protected by a non-zero second Chern number, reminiscent of the characterization of Weyl nodes by the first Chern number.
Type
Publication
Phys. Rev. Lett. 132, 206601 (2024)