Abstract
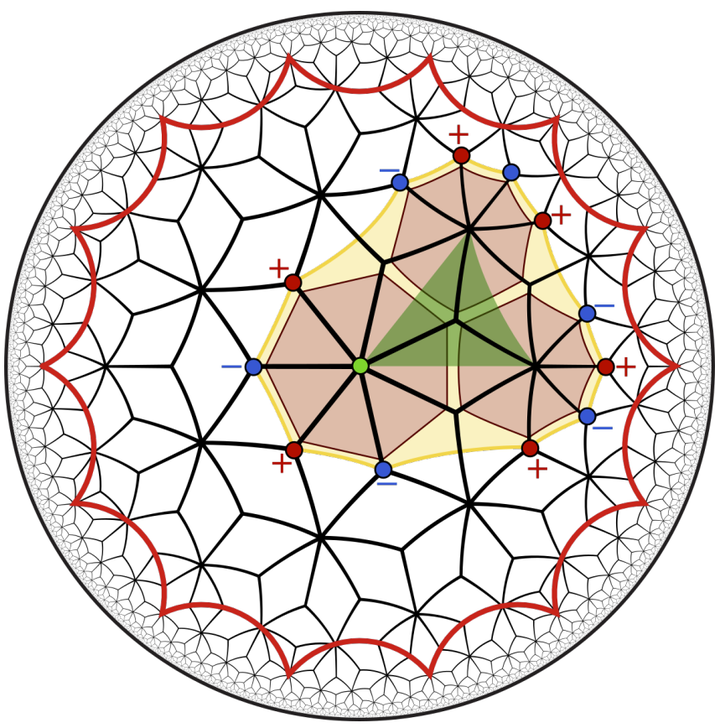
Motivated by the recent experimental realizations of hyperbolic lattices in circuit quantum electrodynamics and in classical electric-circuit networks, we study flat bands and band-touching phenomena in such lattices. We analyze noninteracting nearest-neighbor hopping models on hyperbolic analogs of the kagome and dice lattices with heptagonal and octagonal symmetry. We show that two characteristic features of the energy spectrum of those models, namely the fraction of states in the flat band as well as the number of touching points between the flat band and the dispersive bands, can both be captured exactly by a combination of real-space topology arguments and a reciprocal-space description via the formalism of hyperbolic band theory. Furthermore, using real-space numerical diagonalization on finite lattices with periodic boundary conditions, we obtain new insights into higher-dimensional irreducible representations of the non-Euclidean (Fuchsian) translation group of hyperbolic lattices. First, we find that the fraction of states in the flat band is the same for Abelian and non-Abelian hyperbolic Bloch states. Second, we find that only Abelian states participate in the formation of touching points between the flat and dispersive bands.