Exceptional Topological Insulators
Abstract
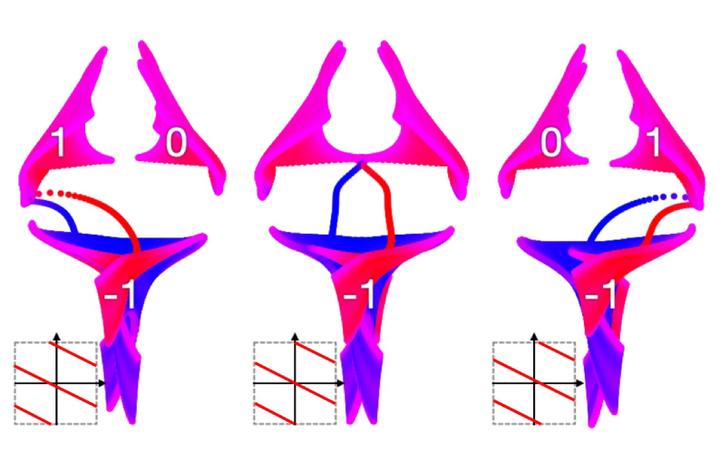
We introduce the exceptional topological insulator (ETI), a non-Hermitian topological state of matter that features exotic non-Hermitian surface states which can only exist within the three-dimensional topological bulk embedding. We show how this phase can evolve from a Weyl semimetal or Hermitian three-dimensional topological insulator close to criticality when quasiparticles acquire a finite lifetime. The ETI does not require any symmetry to be stabilized. It is characterized by a bulk energy point gap, and exhibits robust surface states that cover the bulk gap as a single sheet of complex eigenvalues or with a single exceptional point. The ETI can be induced universally in gapless solid-state systems, thereby setting a paradigm for non-Hermitian topological matter.