Abstract
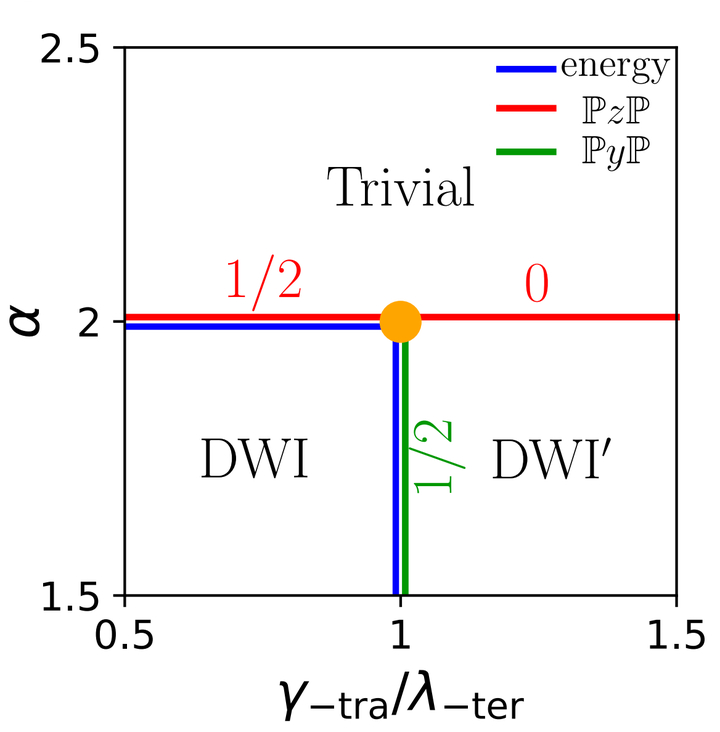
The defining feature of topological insulators is that their valence states are not continuously deformable to a suitably defined atomic limit without breaking the symmetry or closing the energy gap. When the atomic limit is given by symmetric exponentially-localized Wannier orbitals, one finds stable and fragile topological insulators characterized by robust bulk-boundary correspondence. More recently, delicate topological insulators (DIs) have been introduced, whose metallic states are guaranteed only at sharply terminated edges and surfaces. Although Wannierizable, their Wannier orbitals necessarily span multiple unit cells, thus refining the notion of the atomic limit. In this work, we extend delicate topological invariants from Bloch states to hybrid Wannier functions. The resulting models, dubbed delicate Wannier insulators (DWIs), are deformable to unicellular atomic limit in the absence of edges and surfaces; nevertheless, they exhibit obstructions to such deformations as well as topological boundary states in the presence of sharply terminated hinges and corners. We present a layering construction that allows us to elevate a DI in $d$ dimensions into a DWI in $d+1$ dimensions. We illustrate the phenomenology of DWIs by deploying the layering construction on three concrete models.