Abstract
Topological band theory studies the behavior of non-interacting electrons in solids that is protected by topological invariants and is therefore robust against system perturbations. Among many topics that are important for characterizing topological phases of matter, two are greatly relevant for the present work. The first is the stability of topological insulators against addition of trivial bands. Previous studies have identified fragile topological bands, which in contrast to stable topological bands, can be made trivial by adding a filled trivial band (in the language of fermionic band structures). In this thesis, we refine the notion of stability by defining delicate topological bands: they can be trivialized even by adding an empty trivial band above the Fermi level. Crucially, this weaker stability condition allows us to define new topological invariants that otherwise would not be recognized as topologically protected. The second important topic for topological insulators is the attempt to describe them in terms of Wannier orbitals. It is known that stable and fragile topology forms an obstruction to make these orbitals exponentially localized and locally symmetric. We show that delicate topology does not exhibit this ‘strong’ obstruction. Instead, its exponentially localized and symmetric Wannier orbitals can not be localized within one unit cell, which prevents the delicate topological insulator from being deformed to a trivial one. We call such Wannier orbitals multicellular.
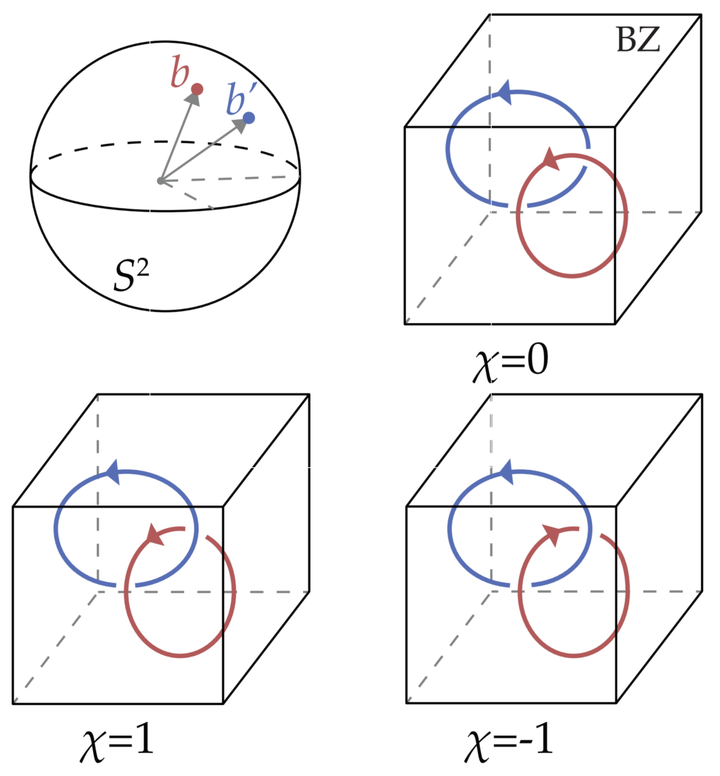
In this thesis, we introduce the concepts of delicate and multicellular topology on the case of crystalline Hopf insulators: two-band three-dimensional insulators invariant under rotation symmetry. We identify the topological invariants characterizing this insulator, the Hopf and the returning Thouless pump (RTP) invariants, and show that they are delicate and multicellular. Moreover, the RTP invariant realizes symmetry-protected delicate topology: it can be trivialized only by addition of trivial bands of specific symmetry representations, while addition of other trivial bands preserves the invariant. This allows us to generalize delicate topological insulators characterized by RTP invariants to Hamiltonians with more than two bands, a step that is important for future materialization of delicate topology. For the specific delicate topological invariants, Hopf and RTP, we derive their bulk-boundary correspondence which realizes a novel way of separating non-trivial bands. For instance, the Hopf invariant induces bands carrying opposite Chern numbers on the opposite surfaces of a finite geometry. This corresponds to a spatial separation of bands with opposite Chern numbers, as opposed to energetic separation of such bands in a Chern insulator. The RTP invariant realizes the first example of ‘conditionally robust’ surface states which are present only at sharp boundaries. Furthermore, we prove that the Hopf and RTP invariants are not completely independent but are related modulo the order of protecting rotation symmetry. This property of delicate topological invariants resembles a similar relation between the Chern number and rotation eigenvalues of stable topological bands. Finally, we discuss an example of a mirror-protected delicate semimetal, showing that the concept of delicate topology can be generalized beyond insulating band structures. Our work on delicate topological phases introduces a new branch in topological band theory and paves the way for further investigation and materialization of delicate topology.