Abstract
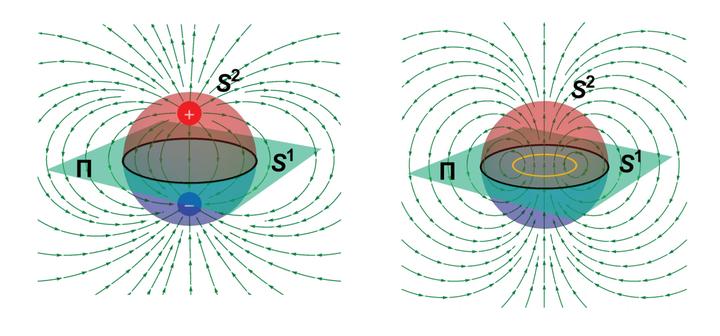
According to a widely held paradigm, a pair of Weyl points with opposite chirality mutually annihilate when brought together. In contrast, we show that such a process is strictly forbidden for Weyl points related by a mirror symmetry, provided that an effective two-band description exists in terms of orbitals with opposite mirror eigenvalue. Instead, such a pair of Weyl points convert into a nodal loop inside a symmetric plane upon the collision. Similar constraints are identified for systems with multiple mirrors, facilitating previously unreported nodal-line and nodal-chain semimetals that exhibit both Fermi-arc and drumhead surface states. We further find that Weyl points in systems symmetric under a π rotation composed with time reversal are characterized by an additional integer charge that we call helicity. A pair of Weyl points with opposite chirality can annihilate only if their helicities also cancel out. We base our predictions on topological crystalline invariants derived from relative homotopy theory, and we test our predictions on simple tight-binding models. The outlined homotopy description can be directly generalized to systems with multiple bands and other choices of symmetry.