Abstract
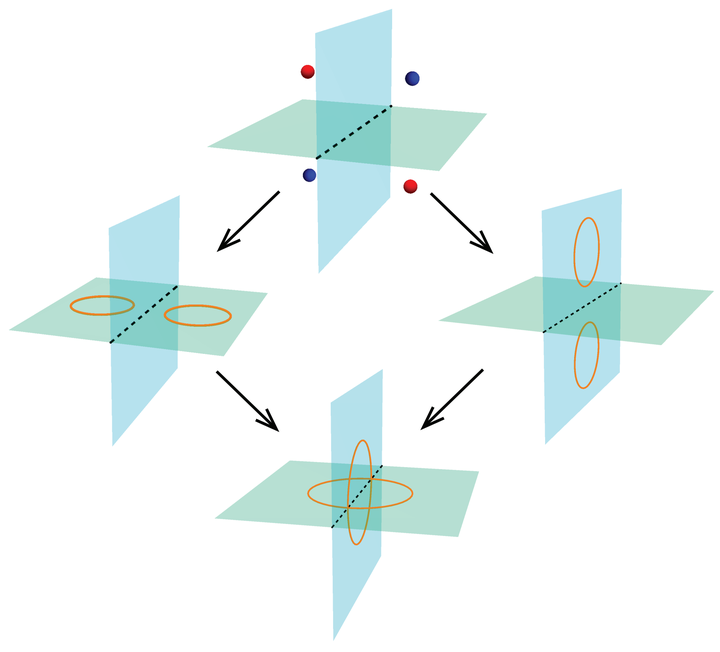
Topological semimetals are characterized by topologically protected band-structure nodes. One prominent example is the Weyl semimetal, characterized by Weyl points carrying topological Chern numbers. In this dissertation, we explore the topology of band-structure nodes with three ingredients: crystal symmetry, nonHermiticity and periodic driving. First, we show that point group symmetry facilitates a new type of topological invariant from relative homotopy theory, which determines the rules for converting generic band nodes to nodes at high-symmetry momenta (and vice versa) as we tune the lattice Hamiltonian. Secondly, we show that exceptional lines in non-Hermitian bands act as Alice strings. This is manifested by the reversal of the topological charge of a node, if it is braided around an exceptional line. Finally, we discuss the Nielsen-Ninomiya no-go theorem in Floquet bands and the possibility of simulating chiral Weyl particles in the adiabatic limit.