Useful code
HyperCells
GAP package that aids in constructing primitive cells and supercells of hyperbolic lattices based on triangle groups and quotients with normal subgroups. For finite systems, this includes the construction of appropriate periodic boundary conditions, while for infinite systems, the corresponding primitive cell and successive supercells are constructed in order to apply the supercell method for hyperbolic band theory. Additionally, the package determines maximally-symmetric Wyckoff positions and simplifies dealing with translation and point group symmetries on the hyperbolic lattice. The package also allows the definition of the graph underlying a specific model, i.e., selecting specific Wyckoff positions, nearest or next-nearest neighbors etc. Check out the file format definitions and the entire documentation.
We have developed a dedicated website that includes installation information as well as several detailed tutorials.
HyperBloch
HyperBloch is a Mathematica package that provides functions for importing and easily visualizing the clusters, supercells, and model graphs output by the HyperCells package. Additionally, it allows the user to easily define tight-binding models ontop of the model graph, by placing orbitals at vertices and defining hopping matrices on the graph edges. Finally, functions for constructing the Abelian Bloch Hamiltonian for the defined model are provided which allows studying eigenstates and eigenvalues.
Check out further information on the dedicated website that also includes installation instructions as well as several detailed tutorials.
Second Chern number
Mathematica code to compute the second Chern number of a four-dimensional (topological) band insulator, downloadable from ResearchGate. The code is an implementation of the algorithm discussed in M. Mochol-Grzelak, A. Dauphin, A. Celi, and M. Lewenstein, Quantum Sci. Technol. 4 014009 (2019), DOI:10.1088/2058-9565/aae93b (where the algorithm's convergence is discussed too).
The data plotted below correspond to $30^4$-partitioning of Hamiltonian:
$$\mathcal{H}(k^\textrm{4D}) = \sum_{i=1}^4 \Gamma_i\sin k_i + \Gamma_5\left[m + \sum_{i=1}^4\cos k_i\right].$$
Patch Euler class
Mathematica code that computes the patch Euler class of a pair of bands on a region (the patch) with a boundary, downloadable from ResearchGate. The patch Euler class is an invariant for systems with $C_2\mathcal{T}$-symmetry (and also for spinless systems with $\mathcal{PT}$-symmetry), which determines whether a pair of Dirac points are able to annihilate along a prescribed trajectory. The algorithm, as described in the supplementary material to A. Bouhon, Q.S. Wu, R.-J. Slager, H. Weng, O. V. Yazyev, and T. Bzdušek, Nat. Phys. 16, 1137–1143 (2020), DOI:10.1038/s41567-020-0967-9 [info], corresponds to a computationally efficient way to extract the most relevant bit of information from the non-Abelian topological invariant introduced previously in Q.S. Qu, A. A. Soluyanov, and T. Bzdušek, Science 365, 1273–1277 (2019), DOI:10.1126/science.aau8740 [info].
The data below plot the Euler curvature computed from first principles near two pairs of band nodes of strained $\textrm{ZrTe}$. Upon pair collision the band nodes are stable in the top scenario, and annihilate in the second scanario – even though no difference is present in the Berry phases and Chern numbers of the scenarios.
Nodal link compositions
Our publications on non-Abelian band topology, first introduced in Q.S. Qu, A. A. Soluyanov, and T. Bzdušek, Science 365, 1273–1277 (2019), DOI:10.1126/science.aau8740 [info], were demanding on visualization of three-dimensional nodal-line compositions. This became especially true in our long overview paper of band topology in $\mathcal{PT}$-symmetric Hermitian band structures through the optics of the non-Abelian band topology, see A. Tiwari and T. Bzdušek, Phys. Rev. B 101, 195130 (2020), DOI:10.1103/PhysRevB.101.195130 [info].
The Mathematica code that generates the plentiful illustrations in the latter paper is downloadable from ResearchGate. The two images below a representative snippet.
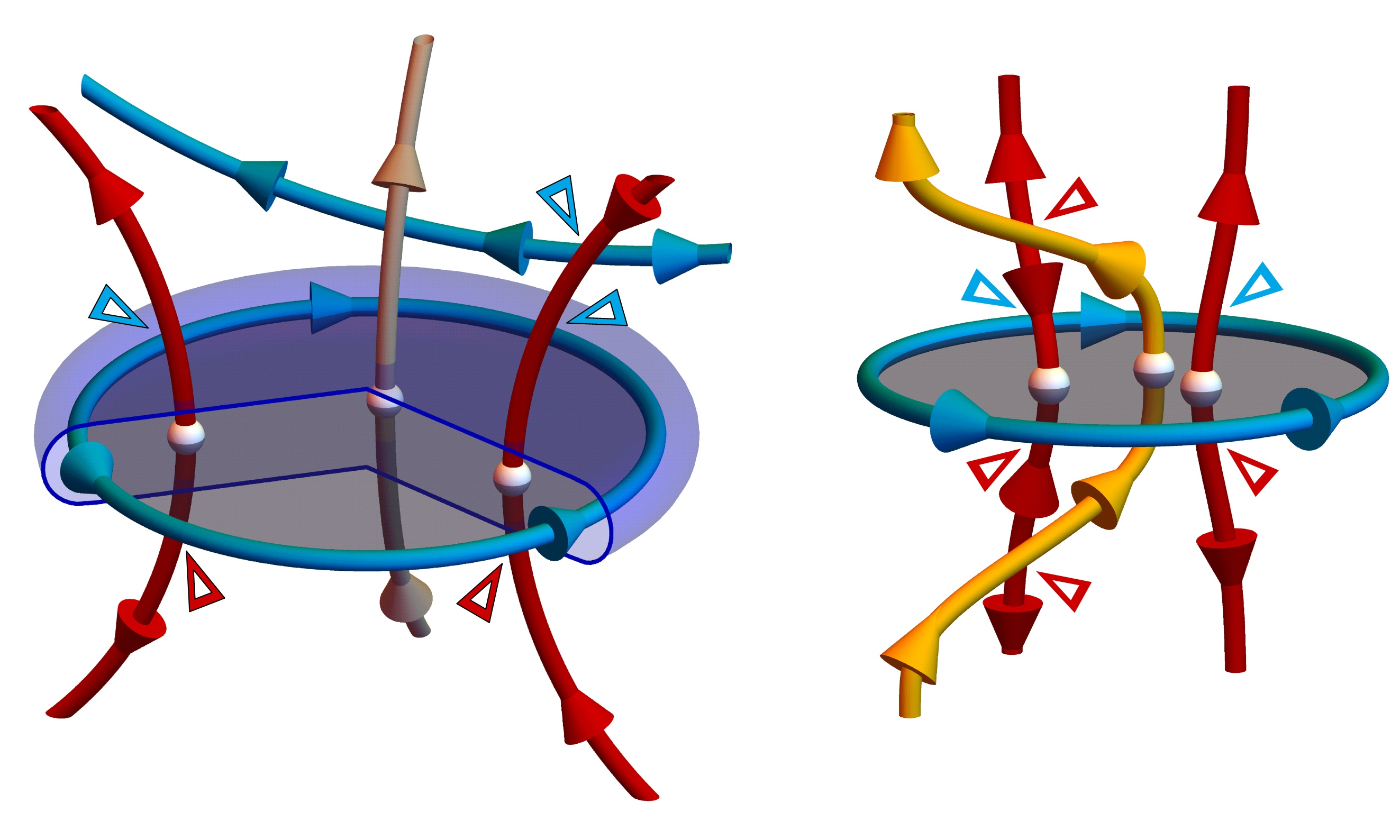
Theses
Doctoral thesis
Symmetry and topology of nodal semimetals (2017)
The work investigates the interplay of crystalline symmetry and topological degeneracies in several classes of nodal semimetals. The thesis is freely accessible at the ETH Research Collection, DOI:10.3929/ethz-b-000216959.
Following the introduction with my insights into topological band theory, the bulk of the work covers three works published during my PhD studies, namely:
- Weyl semimetals in breathing pyrochlore oxides
[T. Bzdušek, A. Rüegg, and M. Sigrist, Weyl semimetal from spontaneous inversion symmetry breaking in pyrochlore oxides, Phys. Rev. B 91, 165105 (2015), DOI:10.1103/PhysRevB.91.165105] - Nodal rings and nodal chains imposed by non-symmorphic symmetry
[T. Bzdušek, Q.S. Wu, A. Rüegg, M. Sigrist, and A. A. Soluyanov, Nodal-chain metals, Nature 538, 75–78 (2016), DOI:10.1038/nature19099] - Homotopy classification of generic band nodes depending on Hamiltonian symmetry
[T. Bzdušek and M. Sigrist, Robust doubly charged nodal lines and nodal surfaces in centrosymmetric systems, Phys. Rev. B 96, 155105 (2017), DOI:10.1103/PhysRevB.96.155105]
The research was done in the group of Manfred Sigrist, and under the further supervision of Andreas Rüegg and Alexey A. Soluyanov. My doctoral thesis was recognized by the Silver Medal of ETH Zürich, and by the Dimitris N. Chorafas Prize by the Dimitris N. Foundation and the Weizmann Institute of Science.
I was awarded the title "DrSc." on 19 Jan 2018.
Master's thesis
Anomalous spectral function of a superconductor (2013)
In superconductors the electron propagator has to be replaced by the Nambu-Gor'kov propagator. The latter is a matrix function, and both the diagonal and the off-diagonal component have Källen-Lehmann spectral representation. While the diagonal spectral function has a probabilistic interpretation and can be readily measured by angle-resolved photoemission spectroscopy, the "anomalous" off-diagonal component is more elusive and at present cannot be experimentally accessed.
In this thesis we studied how pairing and pair-breaking modes in superconductors theoretically lead to markedly different features in the anomalous spectral function, making it potentially a useful tool in determining the pairing glue in unconventional superconductors. We also investigated how the anomalous spectral function could in principle be extracted from the knowledge density-density and spin-spin correlation funcions; however, as the two objects are related by a non-linear transformation, we find that the method is very sensitive to noise and errors in the input data.
The Master's thesis was completed under the supervision of Richard Hlubina, and resulted in the publication of:
- T. Bzdušek and R. Hlubina, What is the pairing glue in the cuprates? Insights from normal and anomalous propagators, Phil. Mag. 95, 609–621 (2015), DOI:10.1080/14786435.2014.980351.
I was awarded the title "Mgr." on 16 Jul 2013.
Bachelor thesis
Study of superconductivity in the disordered Hubbard model (2010)
I was awarded the title "Bc." on 26 Oct 2010.
Recorded talks
Bending the Flatland: Designing classical and quantum matter with non-Euclidean geometry
The inaugural lecture I presented to celebrate my appointment as an SNSF professor at the University of Zürich, delivered on 11 Nov 2024. In the beginning of the video I am introduced by Prof. Titus Nuepert.
On defects, topology, and materials research
An outreach talk (in Slovak language) organized by MatFyz je In and Vedátor_SK. Presented virtually from Zürich (01 Jul 2020).
Non-Abelian band topology in non-interacting metals
Presented at workshop Topomagnetism Is Coming: Relativity and Correlations in Topological Magnets (30 Sep — 03 Oct 2019) at the SPICE center in Mainz.